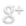Home DNA Ligation

DNA Ligation

Ligation reaction:

Download (PDF, 80KB)

For sticky ends:
x ul DNA insert
y ul DNA vector
2 ul 10x T4 Ligase Buffer  (make sure it is well dissolved)
z ul H2O to 20 ul total
1 ul T4 DNA Ligase (400U/ul)  very temperature sensitive (keep cold at
all times)
10 minutes at RT (20-25C), then put on ice for transformation
For ligations containing blunt ends, this is modfied to 2 hours at RT (see NEB catalog).
For ligations with low amounts of material, this is modified to 14-16 C o/n.
Desired Insert to Vector MOLAR ratio is 3:1
decide on total DNA, t in ng (100 ng is desirable)
x ul of insert =  (3t/ (SizeVec/SizeIns +3)) / [insert]
y ul of vector = (t * SizeVec/SizeIns) / (3 + SizeVec/SizeIns))  / [vector] 
z ul of water = 20 – x – y
where t = total DNA mass (ng) of insert + vector, SizeVec= size of the vector in bp, SizeIns = size of the insert in bp, [insert] is the concentration of the insert in ng/ul, and [vector] is the concentration of the vector in ng/ul.
If volume of insert + vector > 17 ul then set t less than 100ng  (example t = 20 ng)
If there is no insert, then just use 10-100 ng of the vector as x in the reaction.
A more formal description of how to ligate DNA in the context of cloning is here.

 





Blunt
Sticky

[python filename=”ligation2.py”]

 
More information
Use these equations
For a 20 ul reaction:
z=20- x -y -2 -1 = 17 -x- y
z=20-x-y
To calculate volumes x, y, and z, we need to find the mass of X and Y
in ng, and then use the known concentration of X/ul and Y/ul to
calculate volumes x and y.
Desired Insert to Vector MOLAR ratio is 3:1
Want to use 20-200ng total DNA in rxn, aim for 100ng first if possible
i= ng of insert (mass)
v = ng of vector  (mass)
i +v = t ,  where t=100 ng,    t is total mass (equation 1)
(example, t can be substituted with 20-200 ng as needed)
i + v = 100
(moles insert)/(moles vector) =3  (3:1 ratio) (ratio, can be changed, for example use 5:1 for blunt-end cloning) equation 2
i  = moles insert * MWinsert (g/mol) * 109 ng/1g
v = moles vector * MWvector (g/mol) * 109 ng/1g
(i /MW(insert)/(v/MW(vector)) = 3  
     MW is proportional to size
(i / v)  * ((size of vector in bp)/(size of insert in bp))  = 3
SizeIns = size of insert in bp
SizeVec = size of vector in bp
i/v *   (SizeVec/SizeIns) = 3  (equation 2)
solve for I (insert)

i = 3* v (SizeIns/SizeVec)   (equation 3)

so for example if the vector is 3000 bp  and the insert is 1000 bp , then the vector is 3 times bigger than the insert.  Using 100 ng of insert, requires 100 ng of vector to achieve a 3 fold molar excess.
v =  t – i
i/v *   (SizeVec/SizeIns) = 3  (equation 2)
(i/(t-i)) * (SizeVec/SizeIns) = 3  (equation 2a)
solving for i.
i * SizeVec/SizeIns = 3 (t-i)
i * SizeVec/SizeIns = 3t – 3i
i * SizeVec/SizeIns + 3i = 3t
i * (SizeVec/SizeIns  +3) = 3t
i = 3t/ (SizeVec/SizeIns  +3)  (equation 4)
for t=100 ng:
i = 300/ (SizeVec/SizeIns  +3)  (equation 4a)
The corresponding equation is:
use I = T- V to get 

v= (t * SizeVec/SizeIns) / (3 + SizeVec/SizeIns)  (equation 5)

v= 100 * SizeVec/SizeIns) / (3 + SizeVec/SizeIns)  (equation 5a)

i /(concentration of insert) = x ul of insert

Practical equations:

x ul of insert =  (300/ (SizeVec/SizeIns +3)) / insert [concentration](equation 6)

x ul of insert =  (3t/ (SizeVec/SizeIns +3)) / insert [concentration] (equation 6a, general version, where t = total DNA)

y ul of vector = (100 * SizeVec/SizeIns) / (3 + SizeVec/SizeIns)) /vector [concentration] (equation 7) 

y ul of vector = (t * SizeVec/SizeIns) / (3 + SizeVec/SizeIns)) /vector [concentration] (equation 7a, general version, where t = total DNA) 

z ul of water = 20 – x – y  (equation 8) 

If volume of insert + vector > 17 ul then set t less than 100ng  in
equations 3, 4 and 5 (example t = 20 ng)

  • Follow RSI on social media

    Facebook
    Twitter
    Follow by Email
    RSS